03-1 k-최근접 이웃 회귀

이번 챕터에서는 농어의 데이터 중 길이, 높이, 두께가 제공된다.
세 개의 데이터 중 두 개의 데이터로 나머지 하나의 데이터를 예측할 수 있을까?

k-최근접 이웃 회귀

지도 학습 알고리즘은 크게 분류와 회귀(regression)로 나뉜다.
앞 2장에서 배운 분류는 샘플을 몇 개의 클래스 중 하나로 분류하는 것이고
회귀는 임의의 어떤 숫자를 예측하는 것이다.

예를 들면 내년도 경제 성장률을 예측하거나 배달 도착 시간을 예측하는 것이 회귀 문제다.
또한 여기서 주어진 문제처럼 농어의 무게를 예측하는 것도 회귀가 된다.
회귀는 정해진 클래스가 없고 임의의 수치를 출력한다.

2장에서 배운 k-최근접 이웃 알고리즘이 분류뿐만 아니라 회귀에도 작동한다.
분류 알고리즘으로 먼저 예를 들자면,
예측하려는 샘플에 가장 가까운 샘플 k개를 선택하고, 이 샘플들의 클래스를 확인해 다수 클래스를 새로운 샘플의 클래스로 예측한다.
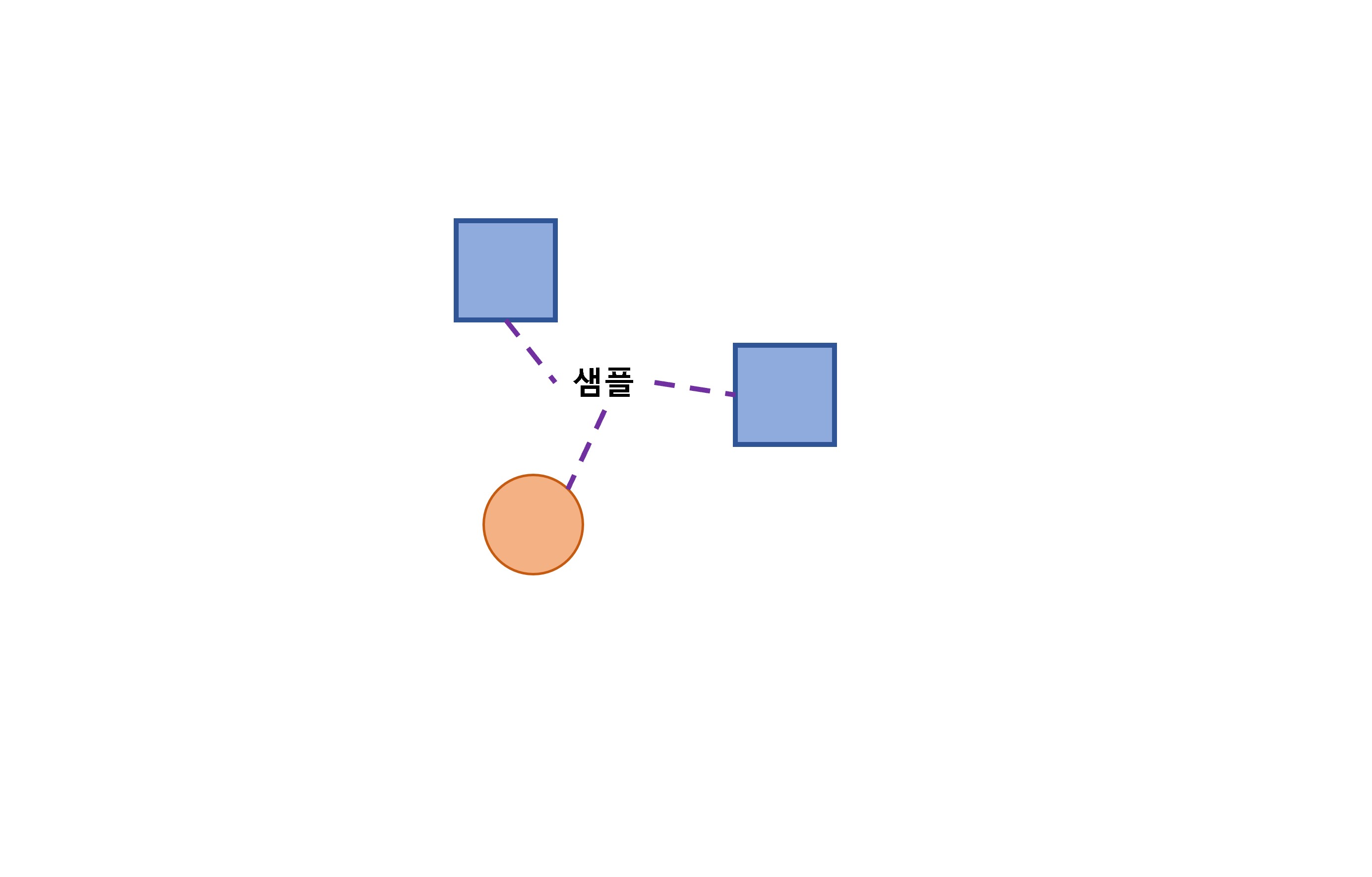위 그림을 예를 들면 k = 3이고, ‘샘플’이란 샘플의 가장 가까운 샘플이 2개의 사각형과 1개의 원이면
사각형이 2개로 다수이기 때문에 ‘샘플’의 클래스는 사각형이 된다.

똑같이 회귀에도 적용을 하면 예측하려는 새로운 샘플에 가장 가까운 샘플 k개를 선택하고
샘플들의 수치로 평균을 구해 새로운 샘플의 타깃을 예측한다.
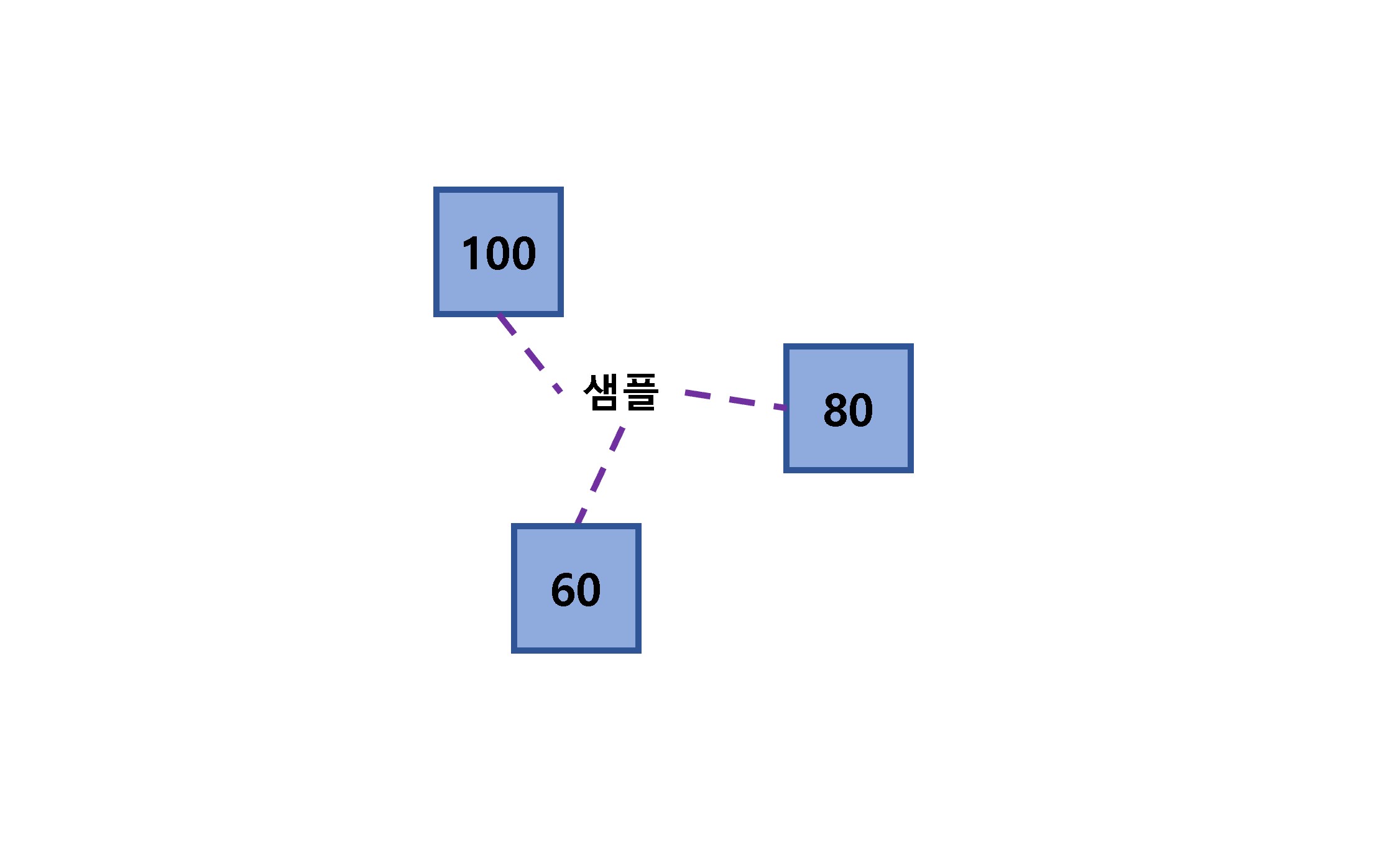위 그림에서 이웃한 샘플의 타깃값이 각각 100, 80, 60이므로 평균은 (100+80+60)/3 = 80, 즉 새로운 샘플의 타깃값은 80이 된다.

그럼 이제 농어의 데이터를 준비하고 사이킷런을 사용해 회귀 모델을 훈련해보자.

데이터 준비

여기선 농어의 길이만 있어도 무게를 예측할 수 있다고 생각했다.
그렇다면 농어의 길이가 특성이고 무게가 타깃이 된다.
넘파이 배열로 바로 만들어보자.

👉 농어의 길이와 무게 데이터

import numpy as np
perch_length = np.array([8.4, 13.7, 15.0, 16.2, 17.4, 18.0, 18.7, 19.0, 19.6, 20.0, 21.0,
       21.0, 21.0, 21.3, 22.0, 22.0, 22.0, 22.0, 22.0, 22.5, 22.5, 22.7,
       23.0, 23.5, 24.0, 24.0, 24.6, 25.0, 25.6, 26.5, 27.3, 27.5, 27.5,
       27.5, 28.0, 28.7, 30.0, 32.8, 34.5, 35.0, 36.5, 36.0, 37.0, 37.0,
       39.0, 39.0, 39.0, 40.0, 40.0, 40.0, 40.0, 42.0, 43.0, 43.0, 43.5,
       44.0])
perch_weight = np.array([5.9, 32.0, 40.0, 51.5, 70.0, 100.0, 78.0, 80.0, 85.0, 85.0, 110.0,
       115.0, 125.0, 130.0, 120.0, 120.0, 130.0, 135.0, 110.0, 130.0,
       150.0, 145.0, 150.0, 170.0, 225.0, 145.0, 188.0, 180.0, 197.0,
       218.0, 300.0, 260.0, 265.0, 250.0, 250.0, 300.0, 320.0, 514.0,
       556.0, 840.0, 685.0, 700.0, 700.0, 690.0, 900.0, 650.0, 820.0,
       850.0, 900.0, 1015.0, 820.0, 1100.0, 1000.0, 1100.0, 1000.0,
       1000.0])

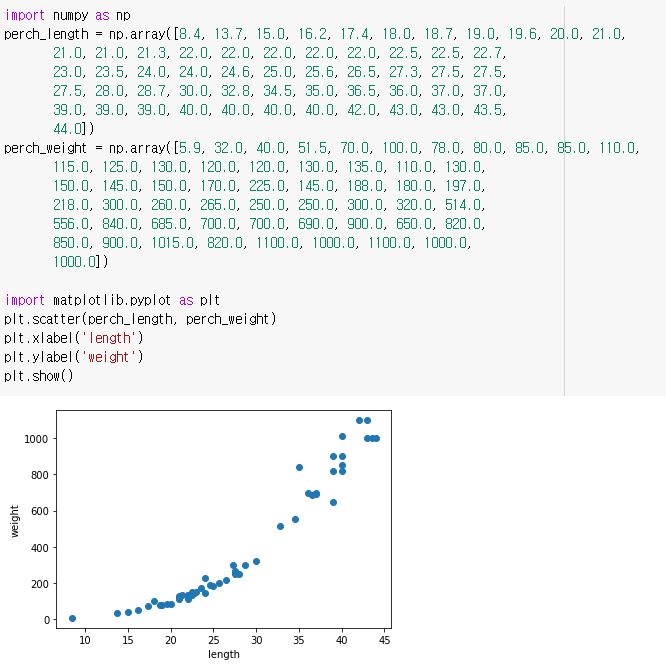
이 데이터들이 어떤 형태를 띠고 있는지 산점도를 그려 확인해보자.

import matplotlib.pyplot as plt
plt.scatter(perch_length, perch_weight)
plt.xlabel('length')
plt.ylabel('weight')
plt.show()

약간 당연하지만 길이가 길어짐에 따라 무게도 늘어나는 것을 알 수 있다.

농어 데이터를 훈련 세트와 테스트 세트로 나누자.

from sklearn.model_selection import train_test_split
train_input, test_input, train_target, test_target = train_test_split(perch_length, perch_weight, random_state = 42)

일관성을 위해 2장처럼 random_state는 42로!!

~~길이와 무게를 한 쌍으로 묶어야 하기 때문에 훈련 세트는 넘파이 2차원 배열이어야 한다.~~
perch_length가 1차원 배열이라서 이걸 나눈 train_input과 test_input도 1차원 배열이라 이걸 다 2차원 배열로 바꿔줘야 한다.

1차원 배열에서 열이 한 개인 2차원 배열로 바꾼다.
(N, )인 1차원 배열을 (N, 1)인 2차원 배열로

넘파이에서 수동으로 배열의 크기를 바꿀 수 있는 reshape() 메서드를 사용해 train_input과 test_input을 2차원 배열로 바꿔보자.

train_input의 크기는 (42, )이고 이걸 (42, 1)로 바꾸려면 train_input.reshape(42, 1) 를 사용해 바꿀 수 있다.
배열의 크기를 아는 경우 이렇게 사용하면 되지만 크기를 따로 확인하지 않고 reshape 하려면
(N, 1)에서 배열의 크기에 해당하는 N에 -1을 넣으면 크기에 맞게 자동으로 변경된다.

두 코드를 비교해보자.

두 코드 다 같은 동작을 한다.
test_input도 2차원 배열로 바꿔줘야 하기 때문에 reshape(-1, 1)을 사용해서 코드를 짜보자.

train_input = train_input.reshape(-1, 1)
test_input = test_input.reshape(-1, 1)
print(train_input.shape, test_input.shape)

성공적으로 2차원 배열로 바꿨다!

결정계수(R²)

k-최근접 이웃 분류 알고리즘을 구현한 클래스는 KNeighborsClassifier 이었고
k-최근접 이웃 회귀 알고리즘을 구현한 클래스는 KNeighborsRegressor 이다.
이 클래스를 사용해 객체를 생성하고 fit() 메서드로 회귀 모델을 훈련하자.

from sklearn.neighbors import KNeighborsRegressor

knr = KNeighborsRegressor()
knr.fit(train_input, train_target)

print(knr.score(test_input, test_target))

1에 근접한 점수가 나왔다.
이 정확하고도 아까운 이 점수는 분류에서는 정답을 맞힌 개수의 비율이었지만 회귀에서는 결정계수(coefficient of determination)라고 부른다.
또는 간단히 R²라고 부른다.
이 값을 구하는 식은 아래와 같다.

각 샘플의 타깃과 예측한 값의 차이를 제곱하여 더하고 타깃과 타깃 평균의 차이를 제곱하여 더한 값으로 나눈 값을 1에서 뺀 값이 결정계수가 된다.

즉 score() 메서드를 통해 나온 값이 결정계수다 !

만약 결정계수가 타깃의 평균 정도를 예측하는 수준이라면 (분모와 분자가 비슷) 0에 가까워지고,
예측이 타깃에 아주 가까워지면 (분자가 0에 가까워짐) 1에 가까운 값이 된다.
첫 번째 경우는 분수가 1에 가까워지기 때문에 1에서 빼면 0에 가까워지는 거고
두 번째 경우는 분수가 0에 가까워지기 때문에 1에서 빼면 1에 가까워지는 거다.

knr.score()로 나온 값인 0.99가 직감적으로 얼마나 좋은지 이해하기가 쉽지 않기 때문에 다른 값을 계산해보자.
타깃과 예측한 값 사이의 차이를 구해 보면 어느 정도 예측이 벗어났는지 가늠하기 좋다.
sklearn.metrics 패키지에서 타깃과 예측의 절댓값 오차의 평균값을 반환하는 mean_absolute_error() 메서드를 사용해보자.

from sklearn.metrics import mean_absolute_error

# 테스트 세트에 대한 예측
test_prediction = knr.predict(test_input)

# 테스트 세트에 대한 평균 절댓값 오차를 계산
mae = mean_absolute_error(test_target, test_prediction)
print(mae)

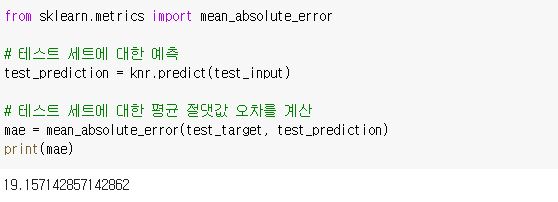
여기서 나온 약 19는 타깃과 예측의 절댓값 오차의 평균이고,
즉 타깃값과 예측이 19 정도 다르다는 것을 의미한다.

지금까지는 훈련 세트를 사용해 모델을 훈련하고 테스트 세트로 모델을 평가했다.
그렇다면 훈련 세트를 사용해 평가해 보는 건 어떨까?
~훈련 세트로 훈련과 평가를 다 한다면 값이 잘 나오지 않을까?~
즉 score() 메서드에 훈련 세트를 전달해 점수를 출력하는 것이다.

과대적합 vs 과소적합

앞에서 훈련한 모델을 사용해 훈련 세트의 R² 점수를 확인해보자.

print(knr.score(train_input, train_target))

훈련 세트로 훈련하고 평가 했는데 값은 훈련 세트로 훈련하고 테스트 세트로 평가한 점수보다 낮게 나왔다.

테스트 세트는 0.99 훈련 세트는 0.96 !?

이렇게 훈련 세트로 훈련했지만 테스트 세트로 평가한 점수가 더 높은 경우를 훈련 세트에 과소적합(underfitting)되었다고 한다.
두 점수가 모두 낮을 경우도 과소적합이라고 한다.
모델이 너무 단순해 훈련 세트에 적절히 훈련되지 않은 경우 과소적합 된다.

반대로 훈련 세트에선 점수가 좋았는데 테스트 세트에서는 점수가 매우 낮으면 훈련 세트에 과대적합(overfitting)되었다고 한다.
훈련 세트에만 잘 맞아서 실전에서 새로운 샘플에 대한 예측을 만들 때 잘 동작하지 않는 다는 것이다

일단 지금과 같은 경우에는 훈련 세트와 테스트 세트의 크기가 매우 작기 때문에 과소적합이 된 것이다.
표본 크기를 늘리기는 어려울 경우엔 모델을 조금 더 복잡하게 만들면 된다.
즉 훈련 세트에 더 잘 맞게 만들면 테스트 세트의 점수는 조금 낮아질 것이다.

k-최근접 이웃 알고리즘으로 모델을 더 복잡하게 만드는 방법은 이웃의 개수 k를 줄이는 것이다
이웃의 개수를 줄이면 훈련 세트에 있는 국지적인 패턴에 민감해지고, 이웃의 개수를 늘리면 데이터 전반의 일반적인 패턴을 따른다.

k-최근접 이웃 알고리즘의 기본 k값은 5이기 때문에 조금 줄인 3으로 낮추어 보자.

knr.n_neighbors = 3

# 바꿨으니 모델 다시 훈련
knr.fit(train_input, train_target)
print(knr.score(train_input, train_target))